permutation parity|arXiv:2408.12881v1 [hep : Bacolod \(S_n\) is a finite group of order \(n!\) and are permutation groups consisting of all possible permutations of n objects. Identity permutation is denoted as \(e\). We will denote a .
Fate/stay night + Sword Art Online/ソードアート・オンライン Crossover. Follow/Fav Fate Revelation Online. By: daniel-gudman. Ilya likes to play video games, and in the time she has remaining, Shirou is more than willing to play the new VR game with her. But when they are trapped inside the game, [Sword Art Online], they determine .
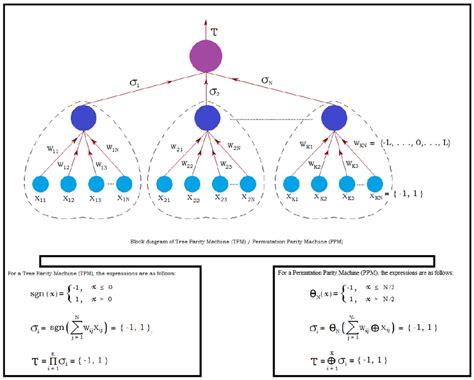
permutation parity,P denotes all permutations of the four up quarks, and p represents the permutation operator. Since all the quarks are the same (all up quarks), the wavefunction simplifies significantly due to the identical nature of the quarks. Thus, for uuuuc¯ .In mathematics, when X is a finite set with at least two elements, the permutations of X (i.e. the bijective functions from X to X) fall into two classes of equal size: the even permutations and the odd permutations. If any total ordering of X is fixed, the parity (oddness or evenness) of a permutation of X can be defined as the parity of the number of inversions for σ, i.e., of pairs of elements x, y of X such . Parity of Permutations and the Alternating Group. A decomposition of permutations into transpositions makes it possible to classify then and identify an .
parity of a permutation from its expression as a product of disjoint cycles: if there are an odd number of cycles of even length then the permutation is odd, otherwise it is even. .permutation is an invertible function that maps a finite set to itself.1 If we specify an order for the elements in the finite set and apply a given permutation to each point in order, .\(S_n\) is a finite group of order \(n!\) and are permutation groups consisting of all possible permutations of n objects. Identity permutation is denoted as \(e\). We will denote a . Thus, if you know how to express any cycle as the product of transpositions, then you know the parity of any permutation. Here's an example. Let $g = (1 \ 2)(3 \ 4 \ . A permutation π of n elements is a one-to-one and onto function having the set {1, 2, ., n} as both its domain and codomain. In other words, a permutation is a .The Parity of a Permutation (Chapter 6, Nos. 32 & 36) The only di erence is that # 32 is about cyclic permutations (one cycle) and # 36 is about any permutation. It turns out .A permutation of the form (m 1 m 2 . m k) is called a cyclic permutation (or cycle) of length k. By definition, (m 1 m 2 . m k) denotes the permutation that carries m 1 into m . A minor variant of the previous answer - copy perm1, and save array lookups. def arePermsEqualParity(perm0, perm1): """Check if 2 permutations are of equal parity.The sign of a permutation $\sigma\in \mathfrak{S}_n$, written ${\rm sgn}(\sigma)$, is defined to be +1 if the permutation is even and -1 if it is odd, and is given by the formula $${\rm sgn}(\sigm.

Parity and number of inversions go together: if the number of inversions is even, so is the parity, and if the number of inversions is odd, so is the parity. Thus, both of these boil down to counting inversions. Every time a larger number precedes a smaller number in a permutation, you have an inversion.permutation parityThis property is called the parity of a permutation, and it is so important that there is a theorem named after it — the Parity Theorem. Unfortunately the proof is somewhat beyond the scope of this blog post, but maybe I will devote a full post to it at some point. In any case, you should now have a good understanding of what it means. Returns true if such a “next permutation” exists; otherwise transforms the range into the lexicographically first permutation (as if by std::sort) and returns false. 1) The set of all permutations is ordered lexicographically with respect to operator < (until C++20) std:: less {} (since C++20).
Computes the parity of a permutation in array form. Explanation. The parity of a permutation reflects the parity of the number of inversions in the permutation, i.e., the number of pairs of x and y such that x > y but p[x] < p[y]. Examples >>>
Given a positive integer \(n \in \mathbb{Z}_{+}\), a permutation of an (ordered) list of \(n\) distinct objects is any reordering of this list. When describing the reorderings themselves, though, the nature of the objects involved is more or less irrelevant. E.g., we can imagine interchanging the second and third items in a list of five .
If a permutation is displayed in matrix form, its inverse can be obtained by exchanging the two rows and rearranging the columns so that the top row is in order. The first step is actually sufficient to obtain the inverse, but the sorting of the top row makes it easier to recognize the inverse. . Parity of Permutations and the Alternating Group.

Parity of a permutation. Every permutation of a finite set can be expressed as the product of transpositions. [43] Although many such expressions for a given permutation may exist, either they all contain an even number of transpositions or they all contain an odd number of transpositions. Thus all permutations can be classified . In this video we discuss the meaning of the parity of a permutation, i.e. whether a permutation is odd or even. We give examples and then prove for the gener.
permutation parity arXiv:2408.12881v1 [hepThe parity of a permutation (as defined in abstract algebra) is the parity of the number of transpositions into which the permutation can be decomposed. [17] For example (ABC) to (BCA) is even because it can be done by swapping A and B then C and A (two transpositions). It can be shown that no permutation can be decomposed both in an . Parity of permutation example. 0. Composition of Permutations. 0. Product of Transpositions Proof. 0. Proof of Group Permutations. 3. parity of given permutation. 0. Parity/sign of the string reversal permutation as a function of length. 0. find parity with inversion of permutation (14)(256) 0.In such a case, ˙is called an odd permutation. Proof: (di erent from book) Show by induction on nthat if ˙= 1 n for transpositions i, then the parity of the number of even-length cycles in ˙equals the parity of n. { Base case (n= 0): ˙consists of zero even-length cycles. { Induction step: Consider what happens when we multiply a permutation ˙=Can you solve this real interview question? Permutations - Given an array nums of distinct integers, return all the possible permutations. You can return the answer . In this lecture we introduce the notion of parity of a permutation and study its properties. In particular we prove that the parity of the product of permuta.
So how does one determine the parity of a permutation? permutations; Share. Cite. Follow edited Jun 9, 2013 at 23:05. Chris Brooks. 7,534 4 4 gold badges 47 47 silver badges 64 64 bronze badges. asked Jun 9, 2013 at 22:52. TheRealFakeNews TheRealFakeNews.arXiv:2408.12881v1 [hep Permutation.parity() : parity() is a sympy Python library function that returns the parity of the permutation. It means the parity of the number of inversions in the permutation. Syntax : sympy.combinatorics.permutations.Permutation.parity() Return : next permutation in lexicographical parity Code #1 : parity() Example
The parity of your permutation is the same as the value of the determinant of this matrix! Luckily, Excel has a built-in determinant function MDETERM(). An even permutation has parity 1 and an odd permutation has parity -1, so you can get the determinant simply with the formula
permutation parity|arXiv:2408.12881v1 [hep
PH0 · arXiv:2408.12881v1 [hep
PH1 · The Parity of a Permutation (Chapter 6, Nos. 32 & 36)
PH2 · Permutations, the Parity Theorem, and Determinants
PH3 · Permutations, cyclic permutations (cycles), permutation groups
PH4 · Parity of permutations
PH5 · Parity of permutation example
PH6 · Parity of a permutation
PH7 · 8.1: Permutations
PH8 · 3.1: Symmetric Groups
PH9 · 15.3: Permutation Groups